top of page

Chapter 7.6 - Similar Polygons
Similar Polygons are exactly the same shape, but can be different sizes.
If polygons are similiar two things will be true:
1. The corresponding interior angles will be the same (congruent)
2. The corresponding sides of each polygon will be the same proportion.
Click here to find more information about similiar polygons
as well as an interactive activity.
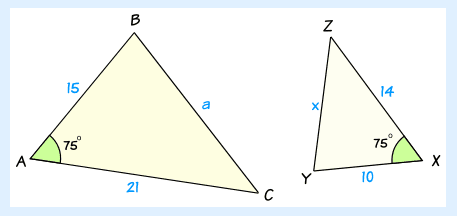
Do you see how both of these rules hold true in these two polygons below.
First Rule - Interior Angles Second Rule - Proportional Sides
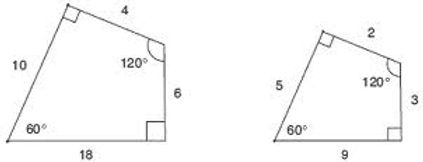

Side lengths and angle measures in similiar figures
Lesson #1 Video Assignment

Indirect Measurements can be used to find the lengths of objects
we may not be able to measure directly.
We can use what we know about similar polygons and proportions
to find the heights of objects like this tree below.
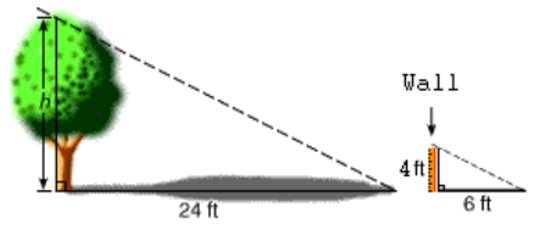
Similar triangles and indirect measurement
Lesson #2 Video Assignment
Similarity Rules for Triangles
(click here for more information)
Triangles are similar if they have:
1. all angles are equal
2. corresponding sides are in the same ratio
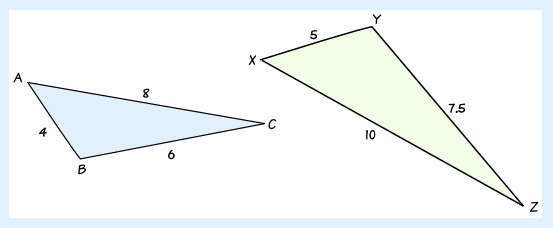
There are three ways to find if two triangles are similar:
1. SSS (side, side, side) - means that we have two similar triangles when all three pairs of corresponding sides in the same ratio.
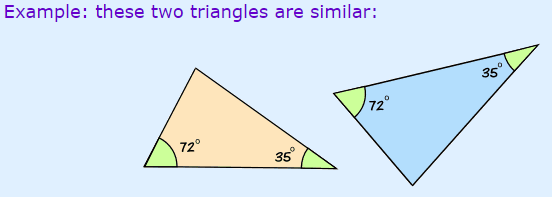
2. AA (angle, angle) - means that we have similar traingles when two of their angles equal.
3. SAS (side, angle, side) - means that we have two similar triangles when:
- two sides are proportional in length
and
- the angle between them is the same
Similarity rules for triangles
Lesson #3 Video Assignment
bottom of page