top of page

Chapter 7.5 - Angles
By the end of this section, you should be able to...
1. Solve problems about angle sums in triangles
2. Use facts about supplementary, complementary, vertical, and adjacent angles to solve multi-step problems
3. Use informal arguements to establish facts about the angles created when two parallel lines are cut by a transversal.
4. Verify experimentally the properties of rotations, refections, and translations.
5. Describe the effects of dilations, translations, rotations, and reflections of two-dimentional figure.
6.Show why a two-dimentional figure is congruent to another if the second can be made throught a series of rotations, reflections, and/or translations (or similar with the above plus dilations).
We can classify angles based on the relationship with other angles.
Complementary angles are two angles whose sum is 90 degrees.
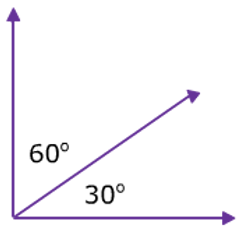
Supplementary angles are two angles whose sum is 180 degrees.

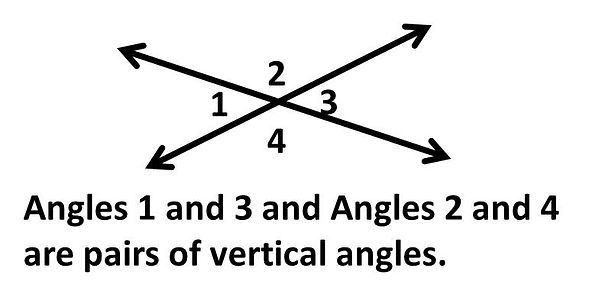
Vertical angles are pairs of angles directly opposite of each other,
formed by intersecting straight lines.
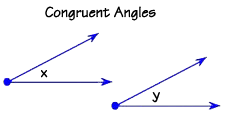
Congruent angles have the exact same measure.
Vertical angles are congruent.
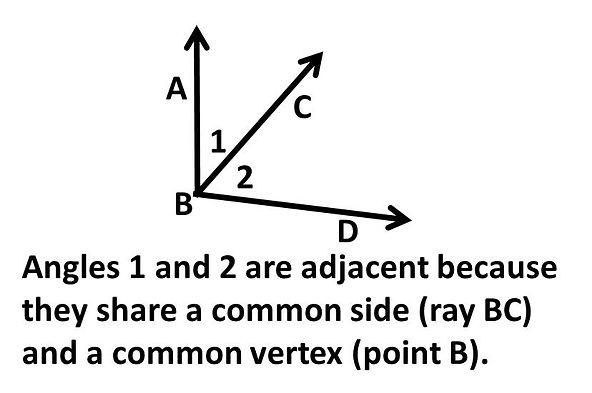
Adjacent angles are angles immediately next to each other.
Identify, complementary, supplementary, vertical, adjacent & congruent angles
Lesson #1 Video Assignment
Now, if I have you the measurements of some angles, could you use what you know about complimentary, supplementary, vertical, adjacent and congruent angles to solve for the unknown angles?
Find measure of complementary, supplementary, vertical, adjacent & congruent angles
Lesson #2 Video Assignment
A transversal is a line that cuts across two or more other lines.
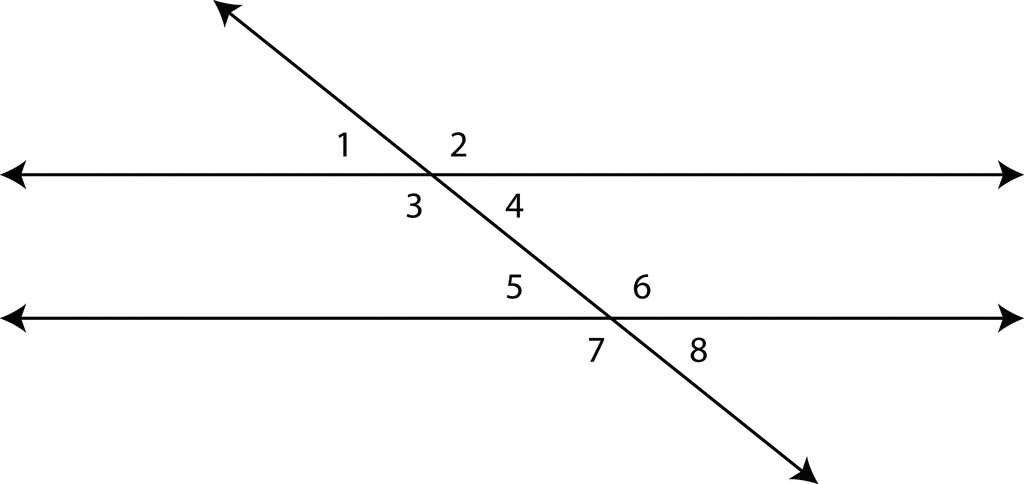
Alternate Interior Angles are angles on opposite side of the transversal
but inside the two lines.
If the lines are parallel, alternate interior angles are congruent.
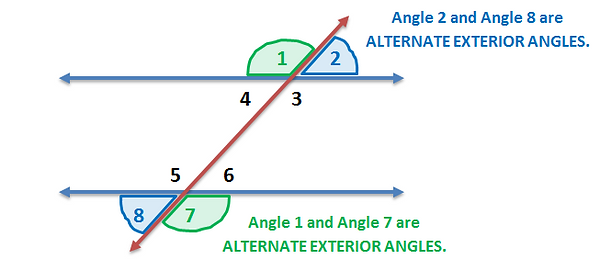
Alternate Exterior Angles are angles on opposite side of the transversal
but outside the two lines.
If the lines ar parallel, alternate exterior angles are congruent.
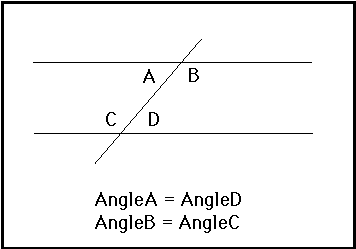
Corresponding angles are angle in matching corners.
If the lines are parallel, corresponding angles are congruent.

Transversal of parallel lines
Lesson #3 Video Assignment
bottom of page